Graph Generation Exploration

In trying to generate an interesting graph for my overworld, I got a bit lost on different techniques. The one I settled on in the end is nothing fancy, though it reminded me of my research days, but for now it serves its purpose: generating a believable enough graph for a story to take place in.

After describing in more details the context of what I set out to do, I want to highlight one of my early attempts, as a cautionary tale that sometimes, fancier is the enemy of good. I will then detail my current solution, simple as it is.

The context

My world is constituted of nodes, belonging to different zones. For now, I have a settled zone, a woodland, a mountainous and a coastal one. For each zone, there are a variety of node types, such as city, castle, farmstead, for the settled zone for instance.

The story will start in a node S of a given type and zone, which will be the start of a journey. The journey will traverse different zones, before reaching the final destination, the goal, a node G of another type. The type of story initially chosen, the way it unfolds, all this will affect the type (and therefore zone) of the target node. It may be that during the story, the goal of the story actually changes - sometimes, the princess is in another castle.

My goal with the graph generation is to generate an interesting path between S and G. Of course, interesting is in the eye of the beholder, but for me, that would imply:

• The path should form a Directed Acyclic Graph going from S to G - no loop back.
• All branches should be approximately of the same length, as to avoid having a shortcut so big that it would render most content meaningless.
• The player should stay in a given zone a reasonable amount of time, neither too long or too short, so that one can explore a varied landscape.
• There should be no wrong path: this is a big one for me, as I intend the story to adapt to the choices, not impose one from the outset. Choosing a different branch will get you potentially harder challenges, but that will come with better outcomes, for instance.
• The transitions from one zone to the next should be as meaningful as possible: this is tricky, but for instance, going from a beach to a mountain top, while technically possible in the Lofoten islands, is not a common scenario that would resonate with most people. A smoother transition from coastal to mountain zone would probably be a valley, or a river.
• There should never be more than four options to choose from, preferably around two to three. In some cases, having only one choice is acceptable (going up a valley, crossing a desert, …) but most of the time it should be between two and three.

Finally, this path, once generated, should be able to map out easily to the travel screen described before, with each choice being laid out from left to right on the screen, represented by a pixel-art drawing.

Attempt #1: Graph Rewriting techniques

I read here and there (lastly in Procedural Generation in Game Design by Tanya X. Short and Tarn Adams) of a technique based on a procedural grammars to generate an interesting-looking graph. The goal is to define a simple grammar, with a starting axiom, and substitution rules. You apply the substitution rules for as long as you do not meet your ending criteria. I do not intend to describe here how such a grammar is defined, but see this video if you want some moving pictures and talking bits or this blog if you want to read.

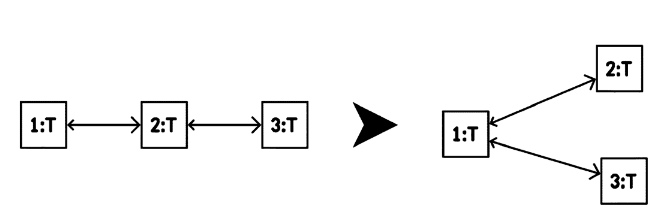
A simple example of an axiom would be: S -> X -> G - where X is any node of any type other than start or end. This is the bare bones description of the graph I want to have. One substitution rule could be X == X -> X, meaning “search everywhere in the graph for a node of any type, and append another node after it”. That would mean to reconnect all the previous successors of X to the second instance. Another rule would be to create a fork of two that reconnects to the previous successors. With these two rules, you can already generate quite a lot of paths, arbitrarily forked.

To restrict the amount of branching that would result in the algorithm repeatedly selecting the same node for the forking rule, you can introduce breaking conditions, that would refuse to apply a rule if the condition is met. A good breaking condition would also be to limit the relative difference between all the branches length.

Finally, I introduced replacement rules to go from X to F, I, M, C (For Forest, Inhabited, Mountains, Coastal), and then also to go from a generic Forest node to a particular one. Already you can probably see how the graph replacement becomes complicated, to handle all the different substitutions and maintain interesting graphs, as per my definition above.

What’s more, I faced a hidden issue - it is one thing to have a graph, but it is another to lay it out flatly on the screen and minimize crossings. Not working with Python, I could not rely of generous and talented souls to have already worked something like this out, and I tried to implement various graph relaxation techniques, that ended up making me feel rather unrelaxed, and gave up. Without a nice layout, the nodes I would place on the left on one screen would end up having their successors all the way to the right on the next screen, which would not have made sense.

The other reason for giving up was that it already took quite some time to come up with this graph replacement, it felt brittle and not very generic - I would have been afraid to add more zones in the future with such a system, and this would have been a big hindrance in the future.

Attempt #2: back to my roots, Markov Chain to the rescue

Back in the days, during my PhD in theoretical cosmology, I developed a Markov Chain Monte Carlo code in Python that my academical brother called Monte Python. It was made to measure the likelihood of various parameters on the standard model for cosmology, by running a simulation of the universe for each point on the parameter space with a code named CLASS. You can’t make that up. It was a nice challenge, and this is by far the output of my PhD that I am the most proud of.

So naturally, after failing with graph replacement techniques, when I stumbled upon Markov Chain methods, I knew that my past had finally caught up with me, and I had to act upon it. In its most essential form, a Markov Chain is just a stochastic (probabilistic) exploration a space. It is not a random walk, instead, you are guided by probabilities. You decide on the next step in your chain of places you visited by looking at the state you are currently in.

In my case, I use it to generate the immediate next neighbors to my current node. So given a node type, I wrote, by hand, meaningful transition weights to another node. This is a good way to introduce some logic in the map making. You want big forest? Make the transition to a forest from a forest have a high probability, and you will end up often with forests that go on and on. To limit the explosion of combinations, I only wrote transition from one node in a zone to another one in the zone - that’s still quite a lot of weights to write, true, but it is more manageable. I did the same from transitioning from one zone to the other, with different weights given to some transitions more likely to happen.

This technique made it extremely simple to satisfy my length constraints for each zone - when I reach my maximum zone length limit, I pick a node from another zone, and then start again. Obviously, this also satisfies that every path is correct, and that there are all more or less the same length - actually, there is only just one path generated, the path not taken will forever be unknown. From the screenshot below, if that was the overworld map for the player, it would be painfully obvious that the rest of the world does not exist, but looking at it from the travel screen, it should not be seen, nor felt.

Finally, the algorithm is simple, and adding more nodes and more zones will be tedious, yes, but not complex. Tedious I can do. I added a few test rules to ensure that all nodes have transition weights, and that all zone transitions are defined.

The resulting graphs look like this. As you can see, the layout question is also removed, as I can take from left to right easily, there will never be crossings, because there is only one path.

It is also, I feel, an apt metaphor for whatever journey you embark on. You will never know what would happen to the other branches you never explored. As far as you’re concerned, your truth is only in the one path you are treading, not the myriad of others you left aside. I like it when a technical solution fits the theme of the implementation - it feels a bit like when a musical movement is in synchrony with the lyrics of the song.

That’s it for this time. It took a long time to write because developing a game as a hobby in the evening after work is not something that is easy to manage on a regular basis. Next time should be to showcase the first results of putting the graph onto the travel screen - for better or worse, that will include my crude attempts at pixel-art… In the meantime, don’t forget to take breaks, but keep creating!